题目背景

提示信息：

质数：是一个大于 $1$ 的自然数，且除了 $1$ 和它本身外，不能被其他自然数整除的数。最小的质数是 $2$，$1$ 不是质数。

合数：一个正整数，如果除 $1$ 和它本身以外，还能被其他正整数整除，叫合数。如 $6$ 是合数，除了 $1$ 和$6$ 以外，还能被$2$ 和$3$ 整除。

分解质因数：每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数，把一个合数用质因数相乘的形式表示出来，叫做分解质因数(分解质因数只针对合数)。如合数 $12=2\times 2\times 3$ 。

分解质因数的方法是先用这个合数的最小质因数去除这个合数，结果若是一个质数就不再除下去；若是一个合数就继续按原来的方法从最小质因数除起，直至最后除得的结果是一个质数 。

例如：

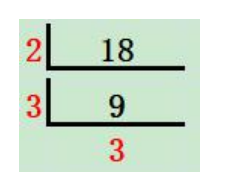
合数 $18$ 分解质因数，首先用最小质因数 $2$ 去除，除后结果为合数 $9$，继续用最小质因数 $3$ 去除，除后结果为质数$3$，就不再除下去。所以 $18$ 的质因数为 $2$、$3$、$3$，故质因数的个数为$3$。

给定一个合数$N$，将$N$ 分解质因数后，输出其质因数的个数。